The general theory of relativity, also known as the general relativity, is a geometric theory of gravity developed by Albert Einstein in 1915. In this theory, he says gravity's effects are a consequence of the curvature of four-dimensional space-time.
For this curvature, the objects in the universe attract each other. This is why planets are orbiting the sun. This curvature is the source of gravity. And in this theory, he also said that in reality gravity is not a force and in fact the same thing as, acceleration.
The general theory of relativity explained
In 1905, Einstein determined that the laws of physics are invariant (or identical) in all inertial (or non-accelerating) frames of reference, and the speed of light in a vacuum is the same for all observers. This was his special theory of relativity.
But objects are not always in the inertial (or non-accelerating) frame of reference they are also in non-inertial (or accelerating) frames of reference. So Einstein trying to include acceleration in his theory. Then he published his general theory of relativity. So in this article, we are going to cover some aspects of general relativity.
Principle of equivalence
Einstein wanted to put an answer to gravity in relative motion and relative time. He wanted to see what gravity is and what its effect is on time and motion.
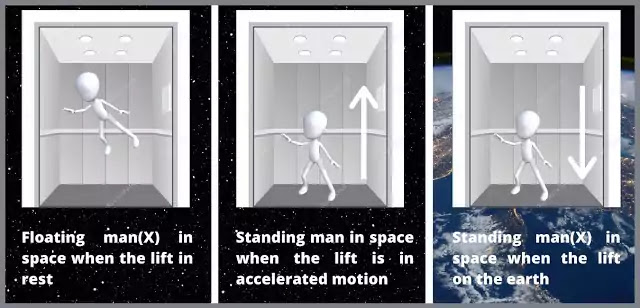
For him, Einstein took the help of a simple thought experiment. He sat in the room, closed his eyes, and thought that there is a lift in space in which there is a person X.
Because the lift is in the space, X floats in this lift. But when the lift is in the earth, the person X always reaches on the floor due to gravity. Now if the lift starts accelerating in space, then person X still reaches on the floor.
This is why Einstein realizes that in reality gravity is not a force and in fact the same thing as acceleration. This is known as the “principle of equivalence”.
Newtonian gravity model
Newton says that two objects in the universe always exert a force of attraction to each other which is known as gravitational force. This force is proportional to the product of the two masses and inversely proportional to the square of the distance between the objects.
According to him, if m1 and m2 be the masses of two objects respectively and r be the separation between them then the gravitational force F between them is
Where G = Universal gravitational constant
Newton said that this gravitational force is an instantaneous force that acting all the time. And if the sun disappears right now, then at the same time the earth will move in the straight path and it will stop rotating around the sun.
Although he told us about the strength of gravity, he never found the source of gravity.
Einstein gravity model
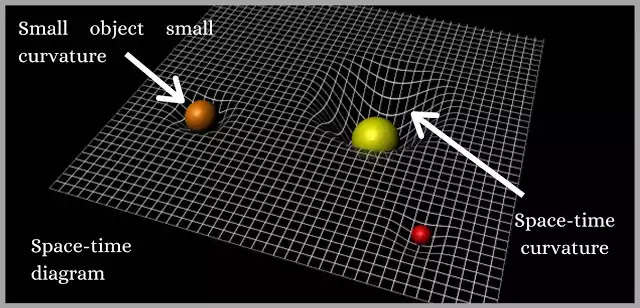
Einstein deeply finds out the source of gravity. He says something like this to explain his gravity model - if you have a sheet, a big ball, and two small-sized balls. Then what will happen when you put the big ball on it, it will push the sheet inwards.
Now if you put two small-sized balls on that sheet, then you will see that both those balls also push the sheet inward but less than the big one.
As the big ball has pushed the sheet more inward, it will pull the small ball inward. Einstein says that this is why the objects in the universe attract each other.
But remember space-time fabric is a 4th-dimensional concept whereas 3 dimensions of space and 1 dimension of time are involved in it. But the simplest way to demonstrate this is with a 2-dimensional fabric. Original space-time fabric looks like this -
According to Einstein's model of gravity, the ripple will be generated in space-time if the sun disappears right now. The speed of these ripples can be equal to the speed of light or less than the speed of light, but never be more than the speed of light. Because in the special theory of relativity Einstein proved that nothing can travel faster than light.
Sunlight arrives on earth at 8 minutes. So if the sun disappears now, the earth will stop rotating 8 minutes after the sun disappears (Because ripples can never exceed the speed of light). As proof of this, many of the stars that ended many years ago are still visible to us.
Einstein Field Equations
As Einstein stated in his principle that "spacetime tells matter how to move, and matter tells spacetime how to curve" means that these quantities must be related to each other.
So he formulated a relation between space-time curvature and matter by using the Riemann curvature tensor and the metric to define another geometrical quantity G, now called the Einstein tensor. This relation is like this -
Where
Gμν = Metric tensor
Tμν = Stress-energy tensor
c = Speed of light in a vacuum
G = Universal gravitational constant
π = The famous constant from geometry
Importance of the general theory of relativity
As in Einstein's special theory of relativity, the theory of the speed of light, the theory of mass-energy equivalence is important. Similarly, In his general theory of relativity, his ground-breaking theories are valuable for the structure of space-time, the equivalence of acceleration, and gravity.
These theories have led to some remarkable consequences, including the time dilation, length contraction, and the bending of light, as well as the prediction of the existence of black holes, wormholes and the “birth” of the universe the big bang.
Experimental evidence
Although instruments can neither see nor measure space-time. But some of the phenomena predicted by its warping have been confirmed. For example - Gravitational lensing, Changes in the orbit of Mercury, Gravitational redshift, Gravitational waves, and black holes.
Changes in the orbit of Mercury
Newton couldn't explain the changes in the orbit of Mercury. But Einstein's gravity model explained it.
He said that actually, the orbit of Mercury is shifting very gradually over time, due to the curvature of space-time around the massive sun. For the validity of Einstein Field Equations, he explained these changes in the orbit of Mercury and did his calculations correctly.