Dimension of Physical Quantity
We know that derived units are such units that depend on base units. For example, if we take the cgs unit of density which is g/cm³. Then it is very easy to understand how the unit of density depends on the unit of length centimeter (cm) and the unit of mass gram (g).
On the other hand, if we take the cgs unit of force (dyne) which is a derived unit, the relationship of the dyne to the base units of length, mass, and time is not directly understood. For this, it is necessary to know how force as a physical quantity relates to length, mass, and time.
Force [F] = [MLT⁻²]
This relation is known as, the dimension of the physical quantity.
From Newton's second law of motion, we know
Force = Mass × Acceleration
∴ Unit of Force = Unit of Mass × Unit of Acceleration
i.e, dyne = g.cm/s² (CGS unit of force)
Here the relation of dyne to the centimeter, gram and second is clearly understood.
Now if we take the dimension of length as L, the dimension of mass M, and the dimension of time as T, then from the above relation we get,
Dimension of Force = Dimension of Mass × Dimension of Acceleration
[F] = [M][LT⁻²]
[F] = [MLT⁻²]
This is the dimension of force which clearly shows how force as a physical quantity depends on the base quantity. So the nature of a physical quantity is also described by its dimensions.
In general, the dimension of a physical quantity is the expression that expresses how any physical quantity depends on base quantities.
Once this dimension is known the relationship of the base units to any derived unit can easily be determined.
All the physical quantities can be expressed in terms of some combination of seven fundamental or base quantities. We shall call these base quantities - the seven dimensions of the physical world.
These base quantities are mass, length, time, temperature, electric current, luminous intensity, and amount of substance.
Where, the mass has the dimension of capital M, length as capital L, time as capital T, temperature as θ, electric current as capital I, luminous intensity as capital J, and amount of substance as capital N.
We have already known the dimensions of seven base quantities. Now let's find the dimensions of other derived quantities.
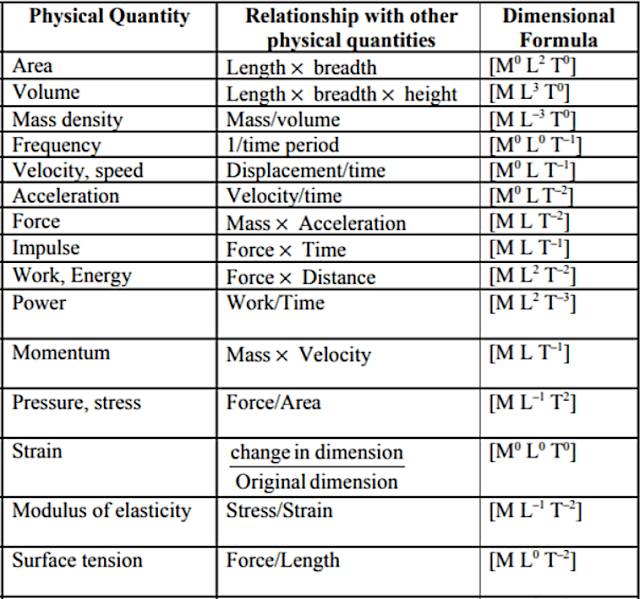
Dimension of Area:
We know, Area = (Length)²
Dimension of [A] = [L²]
Dimension of Volume:
We know, Volume = (Length)³
[V] = [L³]
Dimension of density:
We know, Density = Mass/Volume
Dimension of [ρ] = [M]/[L³]
[ρ] = [ML⁻³]
Dimension of velocity:
We know, Velocity = Displacement/Time
Dimension of [v] = [L]/[T]
[v] = [LT⁻¹]
Dimension of acceleration:
We know, Acceleration = Change in velocity/Time
Dimension of [a] = [LT⁻¹]/[T]
[a] = [LT⁻²]
Dimension of Force:
We know, Force = Mass × Acceleration
Dimension Force [F] = [M][LT⁻²]
[F] = [MLT⁻²]
Dimension of Work:
We know, Work = Force × Displacement
Dimension Work [F] = [MLT⁻²][L]
[F] = [ML²T⁻²]
There are many such derived quantities, but we have listed a few of the, with their relation to base quantities and dimensions.
Dimensionless physical quantity
Some physical quantities are expressed as the ratio of two equivalent physical quantities.
For example, the Plane Angle = Arc/Radius.
Here, both arc and radius refer to length. So both dimensions are L.
i.e the dimension of the plane angle = L/L = 1
Definition: A quantity is called a dimensionless quantity if its dimension is one.
So the plane angle is a dimensionless quantity. Like plane angles, solid angles, specific gravity, etc, are also dimensionless quantities.
Dimension analysis
Definition: Dimension analysis is a method of finding the dependency of derived quantity on base quantities.
Obviously, this is a theoretical analysis.
Three main tasks can be done with this analysis.
1. To change the unit of a physical quantity from one system to another.
2. To check the consistency of a dimensional equation.
3. To determine the correlation of various physical quantities.
The principle upon which these tasks depend is known as the principle of dimensional homogeneity.
This principle states that,
Statement: An equation is dimensionally correct if the different terms on both sides of the equation have the same dimension.
So by analyzing the dimensions of both sides of an equation we can easily understand whether the equation is dimensionally correct or not.
Now let us see whether the following equation taken from four basic kinematics equations is dimensionally correct or not.
Here, x stand for displacement, so its dimension is L. Small u stands for initial velocity, so its dimension is LT⁻¹. Small t stands for time, so its dimension is capital T. And small a stands for acceleration, so its dimension is LT⁻².
So the dimension of the left side of the equation is L.
And the dimension of [ut] = [LT⁻¹] [T] = L
Also, the dimension of [(1/2)at²] = [1] [LT⁻²] [T²] = L
So the dimension of the right side of the equation is L.
As you can see both sides of this equation have the same dimension, so the equation is dimensionally correct. Similarly, by following this method we can easily identify whether any equation is dimensionally correct or not.


Post a Comment (0)