We use the word work in our everyday language to refer to some form of exertion. It may be physical or mental or at times for various activities, such as a farmer plowing the field, a construction worker carrying bricks, a student studying for a competitive examination, or an artist painting a beautiful landscape, all are said to be working.
But in physics, the word "work" covers a definite and precise meaning. In today's lesson, we are going to discuss how physics defines the term work.
Somebody, who can work for 14 to 16 hours a day is said to have a large stamina or energy. We admire a long-distance runner for his/her stamina or energy. Thus energy is our capacity to do work.
In Physics too the term energy is related to work in this sense but as we said the term work itself, is defined much more precisely. So in today's lesson, we explore what is work.
What Is Work?
In Physics, the term work is used in relation to the displacement produced by the force. The work is said to be done only when a body moves under the influence of a force. If there is no motion produced in the body even when a force acts on it the work done is said to be zero.
So work is said to be done only when the force applied on a body makes the body move, that is there is a displacement of the body. Let's understand, with an example.
Consider a constant force F, acting on an object of mass m. The object undergoes a displacement d, in the positive x-direction, as shown in the picture below
The formula for the work done by the force,
Now we see that if there is no displacement no work is done even if the force is large.
Thus, when you push hard against a rigid brick wall the force you exert on the wall does no work. Yet your muscles are alternatively contracting and relaxing and internal energy is being used up and you do get tired.
Expression of Work
It is not always necessary that the force causes displacement of the body in the direction of the force. If under some circumstances a force produces displacement in the body in a direction other than the direction of force, then to determine the amount of work done by the force we have to find the component of displacement of the body in the direction of the force.
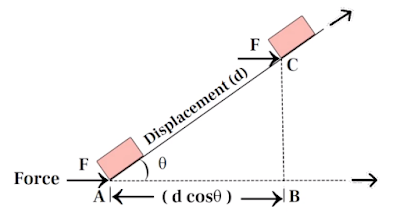
So let us consider a constant force F acts on a body along AB and it displaces the body on an inclined surface such that the point of application of the force moves from A to C.
The displacement of the body AC is equal to small d, which is at an angle θ to the direction of force. In order to calculate the work done by force F we have to find the component of the displacement in the direction of the force.
For that, a perpendicular CB is drawn from C on AB. Then the component of displacement in the direction of force is equal to AB.
Hence work done W = F × AB
But in the right-angled triangle ABC, cosθ = base/hypotenuse, or AB/AC.
Since AC = d, AB = dcosθ
This is the expression of work due to a constant force where the direction of the applied force makes an angle of θ with the direction of the displacement.
Special Cases:
Case 1
If the displacement is in the direction of force i.e. θ = 0°, then cos 0° = 1.
Here, the work done is maximum and positive.
Example:
In the free fall of a body of mass m under gravity through a height h from A to B the force of gravity (F = mg) is in the direction of displacement and the work done by the force of gravity is W = F × d = mgh.
Case 2
If the displacement is normal to the direction of force i.e. θ = 90°, then cos 90° = 0.
∴ W = 0
Hence the work done is zero.
Example:
When a coolie carrying some load on his head moves no work is done against the force of gravity because the displacement of the load being horizontal is normal to the direction of the force of gravity. although coolie does work against the force of friction when he moves with it.
So from these discussions, it is very clear that the amount of work done by a force is zero in the following two situations.
Number 1: When there is no displacement i.e d = 0 and
Number 2: When the displacement is normal, to the direction of the force, i.e. θ = 90°.
Case 3
If the displacement is in a direction opposite to the force i.e. θ = 180 °, then cos 180° = -1.
Here the work done is negative. This is usually the case when the force opposes the motion or it tries to stop a moving body.
Example:
When a body moves on a surface, the force of friction between the body and the surface is in the direction opposite to the motion of the body. So the work done by the force of friction is negative.
Work Done by a Variable Force
The expression for work we saw earlier is only for constant forces. But a constant force is rare it is the variable force that we usually encounter most of the time.
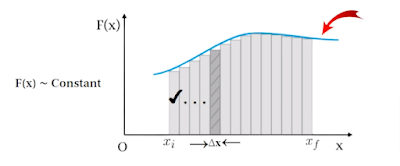
So, let's take a look at the expression for the work done by a variable force. The curved line in the graph shows a varying force in one dimension.
Now if the displacement ∆x is small we can take the force F(x) as approximately constant. Then the work done
Now adding these successive rectangular areas in the picture we get the total work done as
Where the summation is from the initial position xi to the final position xf.
If the displacements are allowed to approach zero then the number of terms in the sum increases without limit but the sum approaches a definite value equal to the area under the curve.
Then the work done
Where limit stands for the limit of the sum when ∆x → 0.
Thus for a varying force, the work done can be expressed as a definite integral of force over displacement. This is the expression of the work done by a variable force.
Units of Work
The SI unit of work is joule.
Since Work = Force × displacement.
Therefore 1 joule = 1 newton × 1 meter
1 Joule: 1 joule of work is said to be done when a force of 1 newton displaces a body through a distance of 1 meter in its own direction.
The CGS unit of work is Erg.
Since Work = Force × displacement.
Therefore 1 joule = 1 dyne × 1 centimeter
1 Erg: 1 Erg of work is said to be done when a force of 1 dyne displaces a body through a distance of 1 centimeter in its own direction.
Dimension of Work
The dimension of work = the dimension of force × the dimension of displacement
The dimension of force = [MLT⁻²] and the dimension of displacement = [L]
Thus the dimension of work = ML²T⁻²



Post a Comment (0)