Scientists have been always curious about the planets, stars, and their motion since ancient times. Nicholas Copernicus was the first to say that the sun is stationary and the earth revolves around the sun. Later, the German scientist Johannes Kepler discovered three elegant laws (Known as Kepler's laws) of planetary motion. By analyzing these formulas, the scientist Sir Isaac Newton determined the nature of the force of attraction between the sun and the planets.

The force of attraction is called gravitation, which is not only between the sun and the planets but also between any two objects or particles in the universe.

What is Gravitation?

The force by which any two objects in this universe attract each other is called gravitation. Newton observed that all the objects in the universe attract each other with a certain amount of force, but in most cases, the force is too weak to observe due to the very large distance of separation.

The range of this force is infinite but the force becomes weaker as the objects move away. To measure this gravitational force, Newton introduced a law in 1680 called Newton's Law of Gravitation or the Universal Law of Gravitation.

What Is Newton's Law Of Gravitation?

According to Newton’s law of gravitation, any two particles in the universe attract each other along their connecting straight lines. The magnitude of this gravitational attraction is

1. Directly proportional to the product of the masses of the two particles and

2. Inversely proportional to the square of the distance between them.

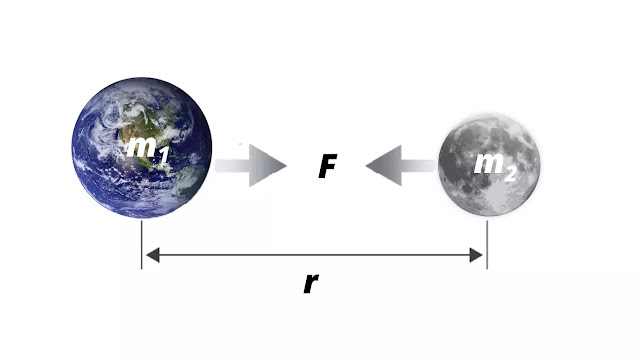
Now let the distance between two particles of mass m1 and m2 be r. If the force of attraction between the two particles is F, then according to Newton's law of gravitation,

$F\propto m_{1}m_{2}\rightarrow \left ( 1 \right )$

$F\propto \frac{1}{r^{2}}\rightarrow \left ( 2 \right )$

Now by combining these two formulas

$F\propto \frac{m_{1}m_{2}}{r^{2}}$

$Or\; F = G\frac{m_{1}m_{2}}{r^{2}}\rightarrow \left ( 3 \right )$

This is the formula of this gravitational attraction between two objects. Here G is the universal gravitational constant.

For the earth and any object on the earth the gravitational attraction

$F=G\frac{Mm}{R^{2}}$

Where M = mass of the earth, m = mass of the object, and R = radius of the earth.

What Is Universal Gravitational Constant?

When m1 = m2 = 1 and r = 1 then from equation no - (3) we can write G = F. It defines the gravitational constant.

Definition: Gravitational constant is the force of attraction between two objects of unit masses separated by unit distance.

Unit: From equation no - (3) we can write

$Unit\;of\; G=\frac{Unit \;of \;F\times (Unit\;of\;r)^{2}}{(Unit\;of\;m)^{2}$

So units of G in the different unit systems are

$In \;the \;SI \;unit \;system\;-\;newton.meter^{2}/kilogram^{2}\;(N.m^{2}/kg^{2})$

$In \;the \;CGS \;unit \;system\;-\;dyne.centimeter^{2}/gram^{2}\;(dyn.cm^{2}/g^{2})$

$In \;the \;FPS \;unit \;system\;-\;poundal.foot^{2}/pound^{2}\;(poundal.ft^{2}/lb^{2})$

Dimension: From equation no - (3) we can write

$Dimension\;of\;G=\frac{Dimension\;of\;F\times (Dimension\;of\;r)^{2}}{(Dimension\;of\;m)^{2}}$

$=\frac{MLT^{-2}\times L^{2}}{M^{2}}$

$=M^{-1}L^{3}T^{-2}$

Magnitude: The value of the gravitational constant determined by various experiments

$Magnitude\;of\;G=6.67\times 10^{-11}\;N.m^{2}/kg^{2}\;(In\;SI\;Unit)$

$=6.67\times 10^{-8}\;dyn.cm^{2}/g^{2}\;(In\;CGS\;Unit)$

$=1.07\times 10^{-9}\;poundal.ft^{2}/lb^{2}\;(In\;FPS\;Unit)$

Read Next: What Is Gravitational Field? #3 Gravitation

Follow Us:

What Is Newton's Law Of Gravitation? #2 Gravitation

What is Gravitation?

What Is Newton's Law Of Gravitation?

What Is Universal Gravitational Constant?

Contact Form