What Is Gravitational Field?
Definition: The gravitational force acting on a unit mass of an object at any point in space is called the gravitational field intensity or gravitational field.
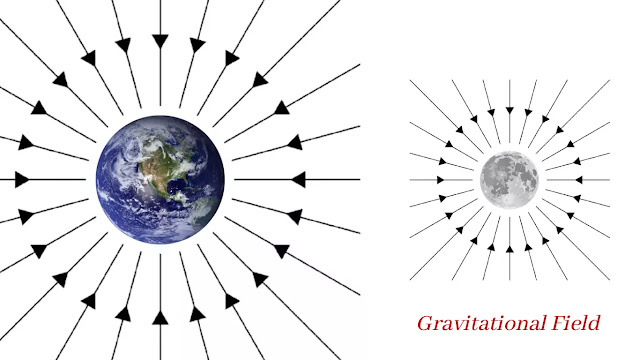
In physics, the gravitational field is a model that is used to explain the influences that a massive object extends into the space around itself, which produces a force on another massive object.
Due to the mass of an object, it creates a field of attractive force around it, and this field of attractive force influences another massive object i.e the region in which an object first exerts a gravitational force on another object is called the gravitational field of the object.
In reality, the gravitational field of any object extends to infinite distances, but the region after which the gravitational force becomes negligible, that region is no longer regarded as the gravitational field of the object.
Formula For Gravitational Field?
It is important not only to mark a region as the gravitational field of an object but also to measure the gravitational effect at each point in that region.
From Newton’s law of gravitation, we know that the gravitational force between two objects of masses M and m separated at a distance of r is
Now for an object of mass M, we need to determine the gravitational field at a distance of r from its center.
So, if we take m = 1 then according to the definition we will get the gravitational field due to the object of mass M at a distance of r from its center, and that is
So from equations no 1 and 2 we get
This is the measure of the gravitational field. From the view of gravitation, this gravitational field intensity is identical to the acceleration due to gravity. So Some time this gravitational field represents as g i.e
Since force and acceleration are both vector quantities, the gravitational field intensity is also a vector quantity. The direction of this field intensity is always worked towards the center of the object.
Unit of Gravitational Field?
From equation no-3 we get the unit of gravitational field i.e
So the unit of this gravitational field is measured in Newtons per kilogram [N/kg] or meters per second squared [m/s2], and dyne per gram [dyn/g] or centimeter per second squared [cm/s2].
Dimension of Gravitational Field?
From equation no-3 we get the dimension of gravitational field i.e
So the dimensional formula of the gravitational field

Post a Comment (0)