What Is Gravitational Potential?
Definition: The amount of work that an external agent has to do to bring an object of unit mass from an infinite distance to a point in the gravitational field is called the gravitational potential of that point.
At infinite distances, that is, where there is no gravitational field, the gravitational potential is taken to be zero. When an object of unit mass is brought from there to a point in the gravitational field, it is acted upon by the gravitational attraction force.
Since the work performed by the force is negative, the gravitational potential is also negative. That is to say, since the gravitational force is always a force of attraction, the gravitational potential at any point in the gravitational field is negative.
Formula For Gravitational Potential
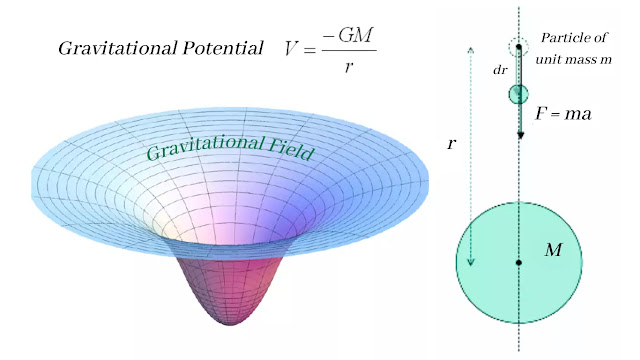
Let's assume an object of unit mass (m = 1) moving freely towards an object of mass M. Here the object of unit mass is attracted by M and move toward it by a small distance dr.
This displacement (dr) is the result of work W exerted by the gravitational field generated by M.
Now we also know from the definition of the gravitational field that the gravitational force due to the object of mass M on a unit mass at a distance of r from its center is
So from equation no-1, we get the work done
Therefore to bring the unit mass from infinity to a position r, the work done or the gravitational potential
This is the measure of the gravitational potential. The relation between the gravitational field and gravitational potential is
Where the gravitational field E = F/m
Since work is a scalar quantity, the gravitational potential is also a scalar quantity.
Unit of Gravitational Potential?
Unit: So the unit of this gravitational potential is measured in joule/kilogram(J/kg) and erg/gram(erg/g).
Read Next: What Is Gravity? #5 Gravitation

Post a Comment (0)