Variations in Acceleration due to gravity

Acceleration due to gravity (g) is not a constant quantity. Its value changes for various reasons, e.g.

• As the earth is elliptical, the value of g varies in different parts of the earth's surface.

• The value of g varies at different heights from the surface of the earth.

• The value of g varies at different depths from the surface of the earth

• It also varies in different parts of the earth's surface due to the rotational motion of the earth.

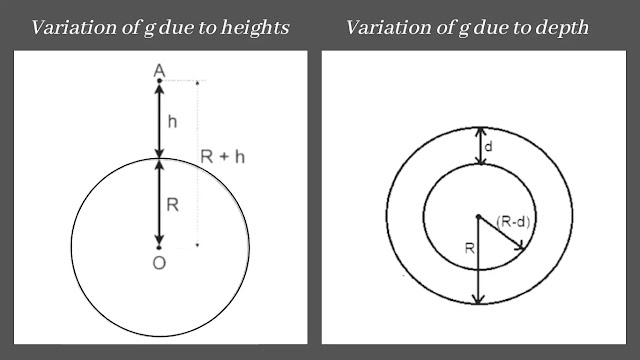
Variation in acceleration due to gravity (#7 Gravitation)

Variation in acceleration due to gravity with heights

Let the earth be a sphere of radius R and mass M. We know the acceleration due to gravity on the surface of the earth is

$g=\frac{GM}{R^{2}}\to (1)$

We will determine the formula for the acceleration due to gravity at a point above the surface of the earth.

So consider any point at the height h above the surface of the earth. The acceleration due to gravity at that point is

$g_{h}=\frac{GM}{(R+h)^{2}}\to (2)$

Dividing equation 2 by 1 we get

$\frac{g_{h}}{g}=\frac{\frac{GM}{(R+h)^{2}}}{\frac{GM}{R^{2}}}$

$or\;\frac{g_{h}}{g}=\frac{R^{2}}{(R+h)^{2}}$

$or\;g_{h}=\frac{R^{2}}{(R+h)^{2}}g$

$\therefore\;g_{h} < g$

★ This means that as we continue to move above the surface of the earth, the acceleration due to gravity decreases.

$Now \;g_{h}=\frac{R^{2}}{R^{2}(1+\frac{h}{R})^{2}}g$

$or \;g_{h}=\frac{1}{(1+\frac{h}{R})^{2}}g$

$or \;g_{h}={(1+\frac{h}{R})^{-2}}g$

Using Binomial Theorem, we get

$or \;g_{h}=g{(1-\frac{2h}{R})}$

This is the formula for variation in acceleration due to gravity with heights.

Variation in acceleration due to gravity with depth

Again let the earth be a sphere of radius R and mass M. We know the acceleration due to gravity on the surface of the earth is

$g=\frac{GM}{R^{2}}\to (1)$

If ρ is the density of the earth, then,

$Density(\rho )=\frac{Mass(M)}{Volume(V)}$

$\therefore\;M=\rho V$

$But,\;V=\frac{4}{3}\pi R^{3}$

$\therefore \;M=\frac{4}{3}\pi R^{3}\rho$

Now substituting the value of M in equation no-1 we get

$g=\frac{G}{R^{2}}\times \frac{4}{3}\pi R^{3}\rho$

$Or\;g=\frac{4}{3}\pi R\rho G\to (2)$

We will determine the formula for the acceleration due to gravity at a point below the surface of the earth.

So consider any point inside the earth below the earth’s surface at depth d. In which, if an object is placed, it will only experience the force due to the portion of the earth of radius (R-d).

Now again let M be the mass of the earth of the portion of radius (R-d) then the acceleration due to gravity at that point is

$g_{d}=\frac{GM'}{(R-d)^{2}}\to (3)$

$But,\;M'=\frac{4}{3}\pi (R-d)^{3}\rho$

$\therefore\;g_{d} =\frac{G}{(R-d)^{2}}\frac{4}{3}\pi (R-d)^{3}\rho$

$Or\;g_{d} =\frac{4}{3}\pi (R-d)G\rho \to (4)$

Dividing this equation 4 by 2 we get

$\frac{g_{d}}{g}=\frac{(R-d)}{R}$

$\therefore\;g_{d} =(1-\frac{d}{R})g$

This is the formula for variation in acceleration due to gravity with depth. It clearly shows that the value of acceleration due to gravity decreases with depth.

★ At the center of the earth d=R, so the acceleration due to gravity at the center is

$g_{d} =(1-\frac{R}{R})g=0$

Read Next: Motions of Planets and Satellites (#8 Gravitation)

Follow Us:

Variation in acceleration due to gravity (#7 Gravitation)

Variations in Acceleration due to gravity

Variation in acceleration due to gravity with heights

Variation in acceleration due to gravity with depth

Contact Form